Source Description:
The dimensions used by Kirov and Williamson 1,2 in their study of the STM source are used here. The STM1251 source consists of a cylindrical gold rod (0.180 mm diameter) inside of a 3.81 mm long aluminum wire with a diameter of 0.510 mm. The aluminum wire is coated with 1.90 μm of nickel, 2.50 μm of copper and 17.0nm of radioactive iodine. The source is encapsulated in a titanium tube with 0.080 mm thick walls, 0.810 mm outer diameter and 0.130 mm thick solid cylindrical end welds. The overall source length is 4.55 mm (Note: 4.50 mm in CLRPv1 database) and the active length is 3.82 mm (Note: the v1 version of this database mistakenly reported the active length as 3.80 mm). The TG43U1 active length is 3.81 mm. The cylindrical source element is free to move 0.240 mm along the seed axis and 0.066 mm radially from the center of the seed, however, we assume it is always centred. The mean photon energy calculated on the surface of the source is 28.44 keV with statistical uncertainties < 0.009%
Dose-Rate Constant - Λ :
Dose-rate constants, Λ , are calculated by dividing the dose to water per history in a (0.1 mm)3 voxel centered on the reference position, (1 cm,Π/2), in a 30x30x30 cm3 water phantom, by the air-kerma strength per history (scored in vacuo). As described in ref. 3 , dose-rate constants are provided for air-kerma strength calculated using voxels of 2.66x2.66x0.05 cm3 (WAFAC) and 0.1x0.1x0.05 cm3 (point) located 10 cm from the source. The larger voxel size averages the air kerma per history over a region covering roughly the same solid angle subtended by the primary collimator of the WAFAC 4,5 at NIST used for calibrating low-energy brachytherapy sources and is likely the most clinically relevant value. The small voxel serves to estimate the air kerma per history at a point on the transverse axis and includes a small 1/r2 correction (0.5%)3. egs_brachy and BrachyDose MC uncertainties are only statistical uncertainties (k=1).
| Author | Method | Λ (cGy h-1 U-1) | Abs. Uncertainty |
| Safigholi et al 6 | WAFAC | 0.9923 | 0.0001 |
| Safigholi et al 6 | Point | 1.0286 | 0.0026 |
| Taylor, Rogers 7 | WAFAC | 1.012 | 0.002 |
| Taylor, Rogers 7 | Point | 1.045 | 0.003 |
| Kirov, Williamson 1 | extrap (PTRAN) | 1.041 | --- |
| Kirov, Williamson 1 | WAFAC (PTRAN) | 0.980 | 0.024 |
| Li, Williamson 8 | TLD | 1.039 | 0.073 |
| Chiu-Tsao et al 9 | TLD | 1.07 | 0.06 |
| Rodriguez, Rogers 10 | TLD Revised (Li) | 0.968 | 0.062 |
| Rodriguez, Rogers 10 | WAFAC (BrachyDose) | 0.992 | 0.0015 |
| Rivard et al 11 | Consensus Value (TG43U1) | 1.018 | --- |
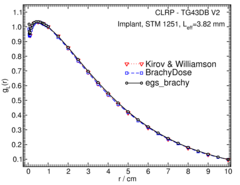
Radial dose function - g(r):
The radial dose function, g(r), is calculated using both line and point source geometry functions and tabulated at 36 different radial distances ranging from 0.05 cm to 10 cm. Fit parameters for a modified polynomial expression are also provided 12 . The mean residual deviations from the actual data for the best fit were < 0.12%.
| Fitting coefficients for g L (r) = (a0 r-2 + a1 r-1 + a2 + a3r + a4r2 + a5 r3) e-a6r | |||
| Fit range | Coefficients | ||
| r min (cm) | r max (cm) | ||
| 0.05 | 10.0 | a0 / cm2 | (9.70+/-0.12)E-04 |
| a1 / cm | (-2.399+/-0.028)E-02 | ||
| a2 | (1.1011+/-0.0016)E+00 | ||
| a3 / cm-1 | (3.94+/-0.12)E-01 | ||
| a4 / cm-2 | (-1.42+/-0.30)E-02 | ||
| a5 / cm-3 | (7.65+/-0.19)E-04 | ||
| a6 / cm-1 | (3.79+/-0.10)E-01 | ||
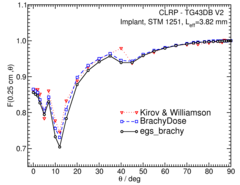
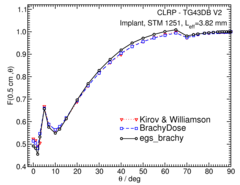
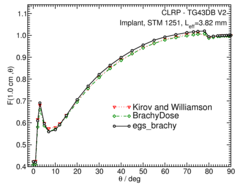
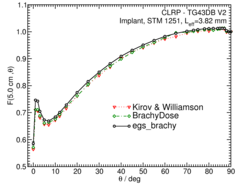
Anisotropy function - F(r,θ):
Anisotropy functions are calculated using the line source approximation and tabulated at radii of 0.1, 0.15, 0.25, 0.5, 0.75, 1, 2, 3, 4, 5, 7.5 and 10 cm and 32 unique polar angles with a minimum resolution of 5 o . The anisotropy factor, φ an (r), was calculated by integrating the solid angle weighted dose rate over 0 o ≤ ϑ ≤ 90 o .
Tabulated data:
Tabulated data are available in .xlsx format: Excel
References:
1. A. S. Kirov, J. F. Williamson, Monte Carlo-aided dosimetry of the Source Tech Medical Model STM1251 I-125 interstitial brachytherapy source, Med. Phys., 28 , 764 - 772, 2001
2. A. S. Kirov, J. F. Williamson, Erratum: ‘‘Monte Carlo-aided dosimetry of the Source Tech Medical Model STM1251 I-125 interstitial brachytherapy source’’ [Med. Phys. 28, 764–772 „2001] Med. Phys., 29, 262- 263, 2002
3. R. E. P. Taylor et al , Benchmarking BrachyDose: voxel-based EGSnrc Monte Carlo calculations of TG--43 dosimetry parameters, Med. Phys., 34 , 445 - 457, 2007
4. R. Loevinger, Wide-angle free-air chamber for calibration of low-energy brachytherapy sources, Med. Phys., 20 , 907, 1993 5. S. M Seltzer et al , New National Air-Kerma-Strength Standards for 125I and 103Pd Brachytherapy Seeds, J. Res. Natl. Inst. Stand. Technol., 108 , 337 - 358, 2003
6. H. Safigholi, M. J. P. Chamberland, R. E. P. Taylor, C. H. Allen, M. P. Martinov, D. W. O. Rogers, and R. M. Thomson, Update of the CLRP TG-43 parameter database for the brachytherapy, to be published (Current calculation) 7.R.E.P. Taylor, D. W. O. Rogers, An EGSnrc Monte Carlo-calculated database of TG-43 parameters, Med.Phys.,35,4228-4241,2008 8.Z.Li,J.F. Williamson, Measured transverse-axis dosimetric parameters of the model STM1251 125I interstitial source, J. Appl. Clin. Med.Phys,3,212-217,2002 9. S. Chiu-Tsao et al, Themoluminescent dosimetry of the Source Tech Medical model STM1251 I-125 seed, Med. Phys., 30, 1735 -1732 , 2003
10. Rodriguez , D. W. O. Rogers, Effect of improved TLD dosimetry on the determination of dose rate constants for 125I and 103Pd brachytherapyseeds,Med.Phys.41, 114301-15, 2014 11. M. J. Rivard et al , Supplement to the 2004 update of the AAPM Task Group No. 43 Report, Med. Phys., 34 , 2187 - 2205, 2007
12. R. E. P. Taylor, D. W. O. Rogers, More accurate fitting of 125I and 103Pd radial dose functions, Med. Phys., 35 , 4242-4250, 2008
Carleton Laboratory for Radiotherapy Physics
CLRP TG-43 Parameter Database V2
May 5, 2020