Source Description:
Dimensions and internal source positions given in the paper by Li 1 are used for the ProstaSeed source 1,2 . The ProstaSeed contains five silver spheres (0.50 mm diameter) which are coated in 125I. As in the study by Li, the 125I is assumed to be of negligible thickness. The five spheres are free to move within the Ti encapsulation which consists of walls with a thickness of 0.050 mm and 0.30 mm thick end welds. The end welds are modelled using a 0.40 mm radius Ti hemisphere overlapped with a 0.350 mm radius air sphere with its center shifted by 0.250 mm relative to the Ti sphere. The overall length is 4.50 mm and the active length is 3.0 mm. The maximum possible displacement of a source sphere is 1.40 mm along the seed axis and 0.10 mm in the radial direction, however, we assume the spheres are always centred. The mean photon energy calculated on the surface of the source is 27.17 keV with statistical uncertainties < 0.009%.Dose-Rate Constant - Λ :
Dose-rate constants, Λ , are calculated by dividing the dose to water per history in a (0.1 mm)3 voxel centered on the reference position, (1 cm,Π/2), in the 30x30x30 cm3 water phantom, by the air-kerma strength per history (scored in vacuo). As described in ref. 3 , dose-rate constants are provided for air-kerma strength calculated using voxels of 2.66x2.66x0.05 cm3 (WAFAC) and 0.1x0.1x0.05 cm3 (point) located 10 cm from the source. The larger voxel size averages the air-kerma per history over a region covering roughly the same solid angle subtended by the primary collimator of the WAFAC 4,5 at NIST used for calibrating low-energy brachytherapy sources and is likely the most clinically relevant value. The small voxel serves to estimate the air kerma per history at a point on the transverse axis and includes a small 1/r2 correction (0.5%) 3 . MC uncertainties are only statistical uncertainties (k=1).
| Author | Method | Λ (cGy h-1 U-1) | Abs. Uncertainty |
| Safigholi et al 6 | WAFAC | 0.9337 | 0.0002 |
| Safigholi et al 6 | point | 0.9365 | 0.0026 |
| Taylor, Rogers 7 | WAFAC | 0.930 | 0.002 |
| Taylor, Rogers 7 | point | 0.932 | 0.003 |
| Li 1 | point (PTRAN) | 0.925 | 0.04 |
| Wallace 2 | TLD | 0.980 | 0.03 |
| Rodriguez, Rogers 8 | TLD Revised (Wallace) | 0.978 | 0.034 |
| Rodriguez, Rogers 8 | WAFAC (BrachyDose) | 0.931 | 0.015 |
| Rivard et al 9 | TG43U1S1 Consensus Value | 0.953 | --- |
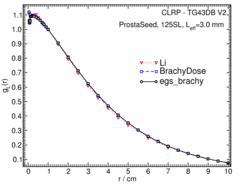
Radial dose function - g(r):
The radial dose function, g(r), is calculated using both line and point source geometry functions and tabulated at 36 different radial distances ranging from 0.05 cm to 10 cm. Fit parameters for a modified polynomial expression are also provided 10 . The mean residual deviations from the actual data for the best fit were < 0.16%.
| Fitting coefficients for g L (r) = (a0 r-2 + a1 r-1 + a2 + a3r + a4r2 + a5 r3) e-a6r | |||
| Fit range | Coefficients | ||
| r min (cm) | r max (cm) | ||
| 0.05 | 10.0 | a0 / cm2 | (6.86+/-0.29)E-04 |
| a1 / cm | (-1.71+/-0.05)E-02 | ||
| a2 | (1.1690+/-0.0020)E+00 | ||
| a3 / cm-1 | (4.37+/-0.05)E-01 | ||
| a4 / cm-2 | (-4.26+/-0.35)E-03 | ||
| a5 / cm-3 | (2.70+/-0.11)E-03 | ||
| a6 / cm-1 | (4.646+/-0.024)E-01 | ||
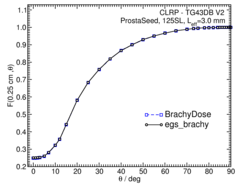
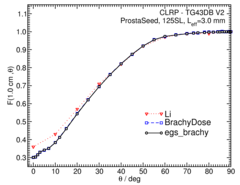
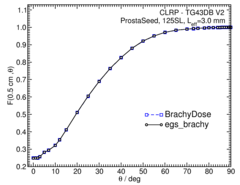
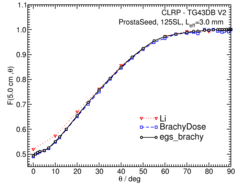
Anisotropy function - F(r,θ):
Anisotropy functions are calculated using the line source approximation and tabulated at radii of 0.1, 0.15, 0.25, 0.5, 0.75, 1, 2, 3, 4, 5, 7.5 and 10 cm and 32 unique polar angles with a minimum resolution of 5 o . The anisotropy factor, φ an (r), was calculated by integrating the solid angle weighted dose rate over 0 o ≤ ϑ ≤ 90 o .
Tabulated data:
Tabulated data are available in .xlsx format: Excel
References:
1. Z. Li, Monte Carlo calculations of dosimetry parameters of the Urocor Prostaseed 125I source, Med. Phys., 29 , 1029-1034, 2002
2. R. E. Wallace, Empirical dosimetric characterization of model I125-SL 125I brachytherapy source in phantom, Med. Phys., 27 , 2796-2802, 2000
3. R. E. P. Taylor et al , Benchmarking BrachyDose: voxel-based EGSnrc Monte Carlo calculations of TG-43 dosimetry parameters, Med. Phys., 34 , 445 - 457, 2007
4. R. Loevinger, Wide-angle free-air chamber for calibration of low-energy brachytherapy sources, Med. Phys., 20 , 907, 1993
5. S. M Seltzer et al , New National Air-Kerma-Strength Standards for 125I and 103Pd Brachytherapy Seeds, J. Res. Natl. Inst. Stand. Technol., 108 , 337 - 358, 2003
6. H. Safigholi, M. J. P. Chamberland, R. E. P. Taylor, C. H. Allen, M. P. Martinov, D. W. O. Rogers, and R. M. Thomson, Update of the CLRP TG-43 parameter database for the brachytherapy, to be published (Current calculation)
7. R. E. P. Taylor, D. W. O. Rogers, An EGSnrc Monte Carlo-calculated database of TG-43 parameters, Med. Phys., 35 , 4228-4241, 2008
8. M. Rodriguez , D. W. O. Rogers, Effect of improved TLD dosimetry on the determination of dose rate constants for 125I and 103Pd brachytherapyseeds, Med.Phys. 41, 114301-15, 2014 9. M. J. Rivard et al, Supplement to the 2004 update of the AAPM Task Group No. 43 Report, Med. Phys., 34 , 2187 - 2205, 2007
10. R. E. P. Taylor, D. W. O. Rogers, More accurate fitting of 125I and 103Pd radial dose functions, Med. Phys., 35 , 4242-4250, 2008